2300 / 3: Long Division, Quotient, Remainder & Calculation Explained - Learn Now!
Can a seemingly simple arithmetic operation unveil complex mathematical principles? The division of numbers, a fundamental pillar of mathematics, holds within its structure a fascinating interplay of quotients, remainders, and diverse calculation methods that shape our understanding of numbers.
The exploration begins with a basic example: dividing 2300 by 3. The outcome of this division provides a foundational understanding of the concept. The quotient (the result of integer division) is 766, and the remainder, representing the "left over" amount, is 2. In this context, 2300 serves as the dividend (the number being divided), and 3 acts as the divisor (the number we are dividing by). Therefore, the answer can be expressed as 766 with a remainder of 2. Understanding these components is the first step in grasping the broader concepts of division.
Let's delve further into these calculations. We can express 2300/3 using a variety of methods. For instance, a calculator might yield a result of 766.6667. Alternatively, we can express the result as a mixed fraction. Moreover, the division of 2300 by 3 produces an outcome that can be approximated to 766.67, the presence of a remainder (2) is key to understanding this aspect. The dividend, which in our example is 2300, is also referred to as the numerator, while the divisor (3 in this instance) is referred to as the denominator. The expression "2300 divided by 3" can be written as the equation: 2300/3. It is crucial to remember that the result is not an exact value and involves remainders.
Now, let's discuss how to use long division. To start, you identify the dividend and the divisor. For a clearer understanding, let's divide 100 by 7. Here, 100 is the dividend and 7 is the divisor. You set up the problem by writing the dividend under a radicand and placing the divisor to its left (divisorvdividend), and then follow the steps involved in long division.
Another example involves 2300 divided by 700. The quotient is 3 with a remainder of 200. Long division with remainders is one of two methods used when solving long division problems by hand.
The long division rules, often explained in a series of steps, are designed for cases where the dividend is a three-digit number and the divisor has two digits. To get started, you establish the dividend (the number to be divided) and the divisor (the number by which you are dividing). This mirrors the common expression, "Divide the dividend x by the divisor y."
The division process often yields repeating patterns, which are commonly called 'reptend.' The notation for these repeating patterns involves overlining the repeating digits with a "vinculum" symbol. Alternatively, parentheses can be used, and in everyday use, an ellipsis may indicate the reptend: 2300 / 6 = 383.3 The division of 2300 by 6 in decimal form is 383, and in fraction form, it is 2300/6. Remember to include one space between the whole number and the fraction.
When working with fractions, such as 3/4 (three-fourths) or 3/100 (three-hundredths), understanding the relationship between numerator and denominator is essential. Similarly, the division of 10 by 5, written as 10/5 or 105 or $ \\frac{10}{5} $, is equal to 2. This is because you can divide 10 into two equal parts, each of size 5. Also, consider the division of 10 by 4, written as 10/4 or 104 or $ \\frac{10}{4} $, which equals 2.5 (2 and a half). This occurs as its possible to create two groups of 4, plus an additional pile of 2, representing half of the four.
Consider examples such as 4 divided by 3, where you get 1 with a remainder of 1. Or, in the case of 25 divided by 2, you get 12 with a remainder of 1. In symbolic notation, the result of such division separates the quotient and remainder with a capital "r". For instance, 8 / 3 = 2 r 2; 4 / 3 = 1 r 1; and 25 / 2 = 12 r 1.
To put these concepts into practice, consider questions like, "What is 20% of 200?" Solutions can be found using our calculator. For instance, consider the division problem: 471 divided by 32. Using our calculator, you'll find that the quotient calculated to three decimal places is 14.718.
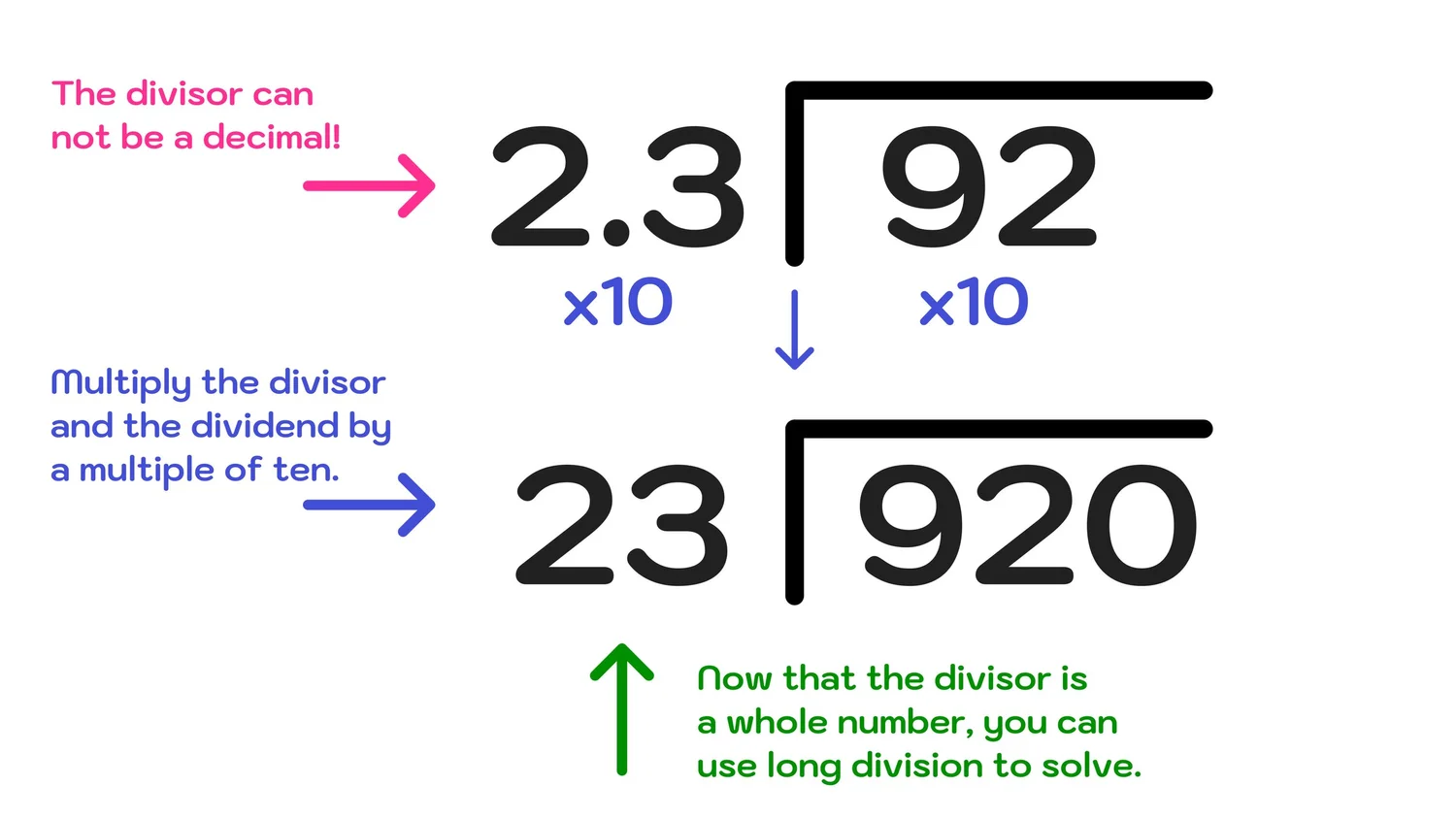
When performing long division involving decimals, as in the division of 4.71 by 3.2, you find the quotient by calculating the answer to three decimal places.
Whether it is addition, subtraction, multiplication, division, square, square root, cube or cube root, all questions can be easily calculated with our user-friendly web calculator.